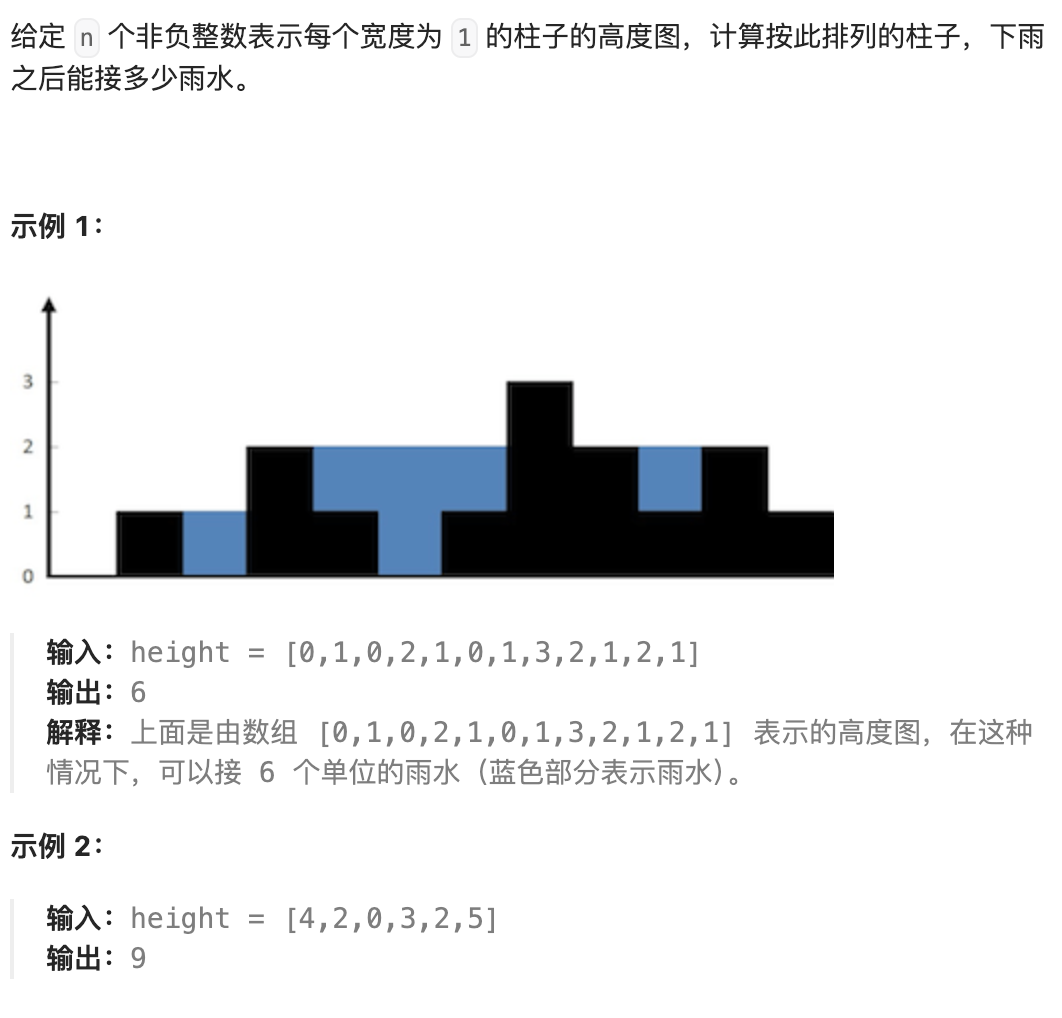
接雨水#
每个位置能接的雨水由左右最高墙得到:
w = max(0, min(leftmax(i), rightmax(i)) - height[i])
问题转换成,如何高效得到 leftmax(i) 和 rightmax(i)。
可以从两端向中间收缩,维护 leftMax 和 rightMax
如果 height[l] < height[r] 那么 l 的可接水上限由 leftMax 决定:
- 如果 height[l] >= leftMax: 更新 leftMax,不做任何处理,因为这个时候一定是接不到水的。
- 否则 leftMax - height[l] 就是 l 位置可接水的量,为什么是这样?这里解释下,由于 rightMax > height[r],而 height[r] > height[l],但是 height[l] < leftMax,所以 leftMax < rightMax
- 然后 l++
java 解法#
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| class Solution {
public int trap(int[] height) {
if (height.length < 3) {
return 0;
}
int l = 0, r = height.length - 1;
int leftMax = 0, rightMax = 0;
int ans = 0;
while (l < r) {
if (height[l] < height[r]) {
if (height[l] >= leftMax) {
leftMax = height[l];
} else {
ans += leftMax - height[l];
}
l ++;
} else {
if (height[r] >= rightMax) {
rightMax = height[r];
} else {
ans += rightMax - height[r];
}
r --;
}
}
return ans;
}
}
|
Python 解法#
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
| class Solution:
def trap(self, height: List[int]) -> int:
n = len(height)
if n < 3:
return 0
l, r = 0, n - 1
left_max = right_max = 0
ans = 0
while l < r:
if height[l] < height[r]:
if height[l] >= left_max:
left_max = height[l]
else:
ans += left_max - height[l]
l += 1
else:
if height[r] >= right_max:
right_max = height[r]
else:
ans += right_max - height[r]
r -= 1
return ans
|
JS 解法#
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
| var trap = function(height) {
const n = height.length;
if (n < 3) return 0;
let l = 0, r = n - 1;
let leftMax = 0, rightMax = 0;
let ans = 0;
while (l < r) {
if (height[l] < height[r]) {
if (height[l] >= leftMax) {
leftMax = height[l];
} else {
ans += leftMax - height[l];
}
l ++;
} else {
if (height[r] >= rightMax) {
rightMax = height[r];
} else {
ans += rightMax - height[r];
}
r --;
}
}
return ans;
};
|
Go 解法#
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
| func trap(height []int) int {
n := len(height)
if n < 3 {
return 0
}
l, r := 0, n-1
leftMax, rightMax := 0, 0
ans := 0
for l < r {
if height[l] < height[r] {
if height[l] >= leftMax {
leftMax = height[l]
} else {
ans += leftMax - height[l]
}
l ++
} else {
if height[r] >= rightMax {
rightMax = height[r]
} else {
ans += rightMax - height[r]
}
r --
}
}
return ans
}
|