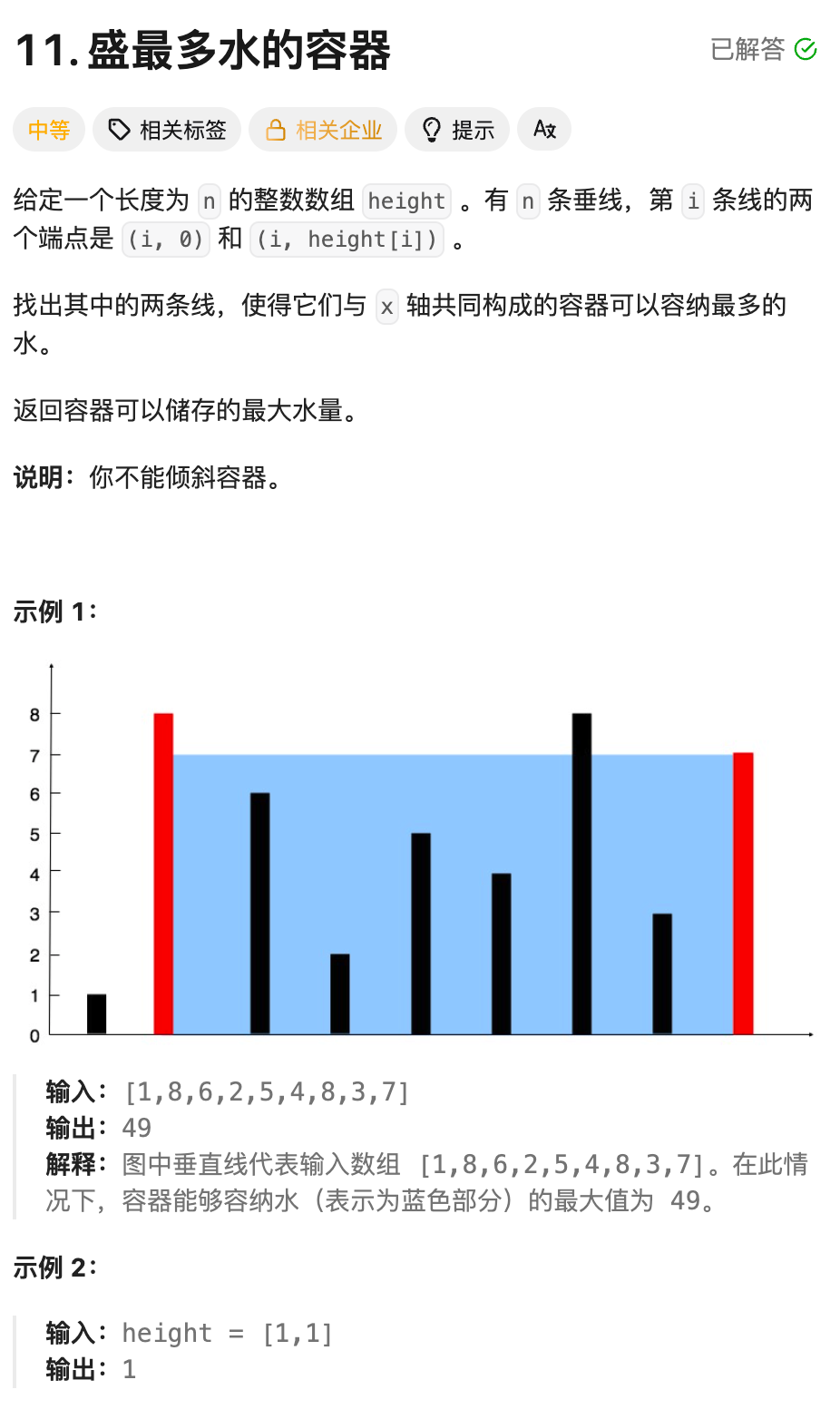
假设左端点在 L,右端点在 R。
那么面积为 (R - L) * min(height[L], height[R])
假设 height[L] < height[R],我们保持左端点不动,移动右端点,那么 min(height[L], height[R]) 也保持不同, (R-L),变小,那么目前的面积是以 L 为左端点的最大面积。
假设存在比当前面积更大的面积,那么 L 不可能是左端点,我们需要找到其他的左端点,使得面积尽可能大。
为了搜索左端点,我们需要将 L 往右移,使得 min(height[L], height[R]) 最大。
所以这道题实际上是对二层 for 循环的优化,每次批量剪枝掉一批答案,使得时间复杂度降低。
Java 解法#
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| class Solution {
public int maxArea(int[] height) {
int l = 0, r = height.length - 1;
int ans = 0;
while (l < r) {
int h = Math.min(height[l], height[r]);
int area = (r - l) * h;
if (area > ans) {
ans = area;
}
if (height[l] < height[r]) {
l ++;
} else {
r --;
}
}
return ans;
}
}
|
Go 解法#
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
| func maxArea(height []int) int {
l, r := 0, len(height) - 1
ans := 0
for l < r {
h := height[l]
if height[r] < h {
h = height[r]
}
area := (r - l) * h
if area > ans {
ans = area
}
if height[l] < height[r] {
l ++
} else {
r --
}
}
return ans
}
|
- Go 语言中没有 while 循环,但是可以用 for 代替 while 循环
l, r := 0, len(height) - 1 的赋值方式在 Go 语言中很常见
python 解法#
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| class Solution:
def maxArea(self, height: List[int]) -> int:
l, r = 0, len(height) - 1
ans = 0
while l < r:
h = min(height[l], height[r])
ans = max(ans, (r-l) * h)
if height[l] < height[r]:
l += 1
else:
r -= 1
return ans
|
JS 解法#
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
| /**
* @param {number[]} height
* @return {number}
*/
var maxArea = function(height) {
let l = 0, r = height.length - 1;
let ans = 0;
while (l < r) {
const h = Math.min(height[l], height[r]);
ans = Math.max(ans, (r-l) * h);
if (height[l] < height[r])
l ++;
else
r --;
}
return ans;
};
|